1984/9 No.6 |
1. 左右性について | 3. ルーバーによる道路騒音対策 | 4. 震動ピックアップの絶対校正 | 5. 音響インテンシティ法による応用計測例 | 6. 聴力と年令 | ||||
リオン㈱音測技術部 小 白 井 敏 明
1、概要
音を大きさと方向を持つ量として扱う事のできる手法、これが音響インテンシティ(Sound Intensity)測定法の大きな特長である。この測定で必要とされる量は、流体中の一点での瞬時音圧と瞬時粒子連度でこの積は瞬時的なインテンシティベクトルとなり、一般的には時刻と共に大きさと方向が変化する。インテンシティは単位時間に単位面積を通過する音のパワーである。
音響インテンシティの測定原理は、1932年頃H. F. OLSONによって示され、以後計測の開発が進められてきたが、最近のエレクトロニクスの進歩によりようやく実現するに至り、急速に普及してきている。特に音響パワーレベルの測定法への音響インテンシティの導入に関して、ISOを中心に検討がなされている。しかし、インテンシティの特長は、単にパワーレベルを簡便に測定する以外に、音の発生状況を詳細に表現してくれることである。この一面は機械設計と放射音との関連性への有益な情報提供となる。以下に計測原理を簡単に述べ、リオンSA-73を用いた応用計測例を紹介する。
応用計測の一つに特に基礎実験的なものとして、アルミ板による振動モードと放射音パターンの関係を示し、更にStructure Borne Wave Intensityと呼ばれる振動のインテンシティ計測から、板上の音の放射位置を直接測定した例を示す。この例は音の放射と振動との関係をよく表現していると考えられ、インテンシティ計測の他方の最大の特長であろう。
2、計測原理
2・1 音響インテンシティ
![]() だけ離れた2個のマイクから瞬時音圧レベルを
だけ離れた2個のマイクから瞬時音圧レベルを![]() 、
、![]() とおくと、r方向のインテンシティベクトルは
とおくと、r方向のインテンシティベクトルは
![]()
周波数領域で、クロススペクトラム法によりインテンシティスペクトラムを求めると、
![]()
本器は(2)式を用いており、次式(3)による位相修正が可能である。
![]()
但し∫:媒体密度、![]() 、
、![]() 、
、![]() は周波数、
は周波数、![]() は音速、
は音速、![]() はランダムノイズを両チャンネル同時に加えた時の伝達関数、
はランダムノイズを両チャンネル同時に加えた時の伝達関数、![]() はランダムノイズ入力時の感度である。
はランダムノイズ入力時の感度である。
2・2 振動インテンシティ
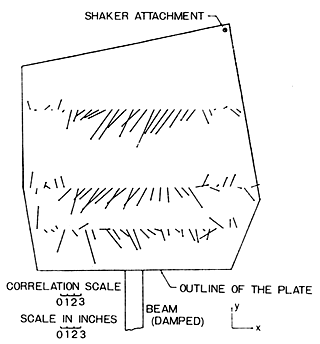
Noiseux (1)は均一材質の板、棒の振動エネルギー流(Power Flow)を測定した。(図1参照)X方向での振動インテンシティWxは、Pure Tone Waveの時
![]()
但し、![]() :スティフネス
:スティフネス ![]() :板の表面密度
:板の表面密度 ![]() :加速度(X方向の直角方向)
:加速度(X方向の直角方向) ![]() :X方向の角速度である。図1は右側上部端部をバンドノイズで加振した場合のPower Flowベクトルで、下端部にビームを付けて制振した時、ベクトルがビーム側に向っている事を示している。
:X方向の角速度である。図1は右側上部端部をバンドノイズで加振した場合のPower Flowベクトルで、下端部にビームを付けて制振した時、ベクトルがビーム側に向っている事を示している。![]() だけ離れた2個の加速ピックアップを剛体結合し、その中央部を振動体に固定する。この時の出力を
だけ離れた2個の加速ピックアップを剛体結合し、その中央部を振動体に固定する。この時の出力を![]() 、
、![]() とすると、
とすると、
![]()
と近似できる。(4)、(5)式より
![]()
(6)式は(2)式を用いて部分的に計算出来る事がわかる。本器では(6)式により実験的な測定を行ない、音響インテンシティとの対応を試みた。
 |
3、インテンシティ応用計測例
処理部の専用ソフトを用いて計測した計測例を以下に示す。
3・1 ガラス窓(1枚ガラスと2枚ガラス)の透過音の比較
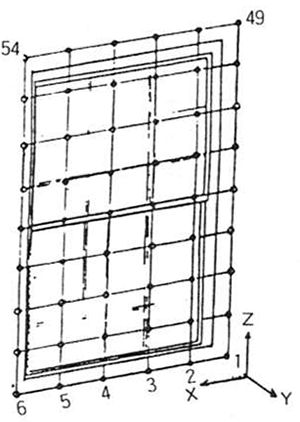
図2の窓の一方にランダムノイズ源を置き、窓を境とした反対面で透過音を測定した。測定は窓に直角方向にマイクを向け、図の様に54点の測定を行なった。
 |
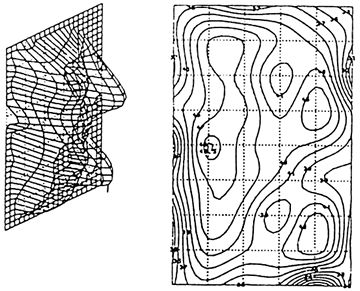 |
1/3OCT. 1.25kHz. 49.6〜40dB |
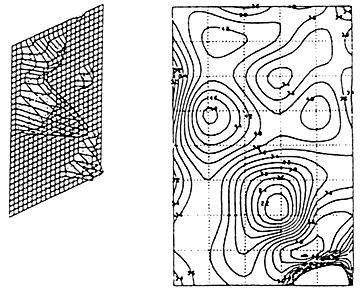 |
1/3OCT. 1.25kHz. 48.5〜40dB |
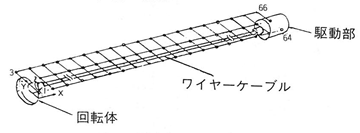
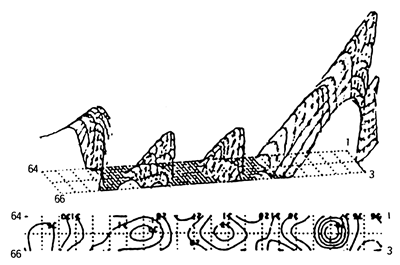
細いチューブ中のワイヤが回転する時の摺動音の測定例。1/3OCT 1.6kHz 成分音の分布で一見して発生部位がわかる。レベルは41〜31dBの範囲で表示。
 |
 |
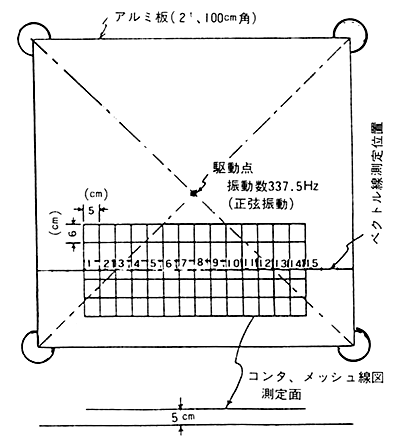
アルミ板(
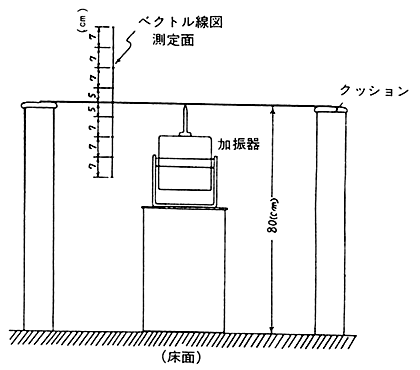 |
|

|
 |
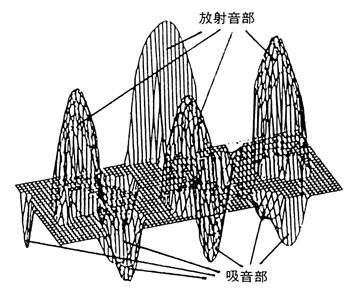 |
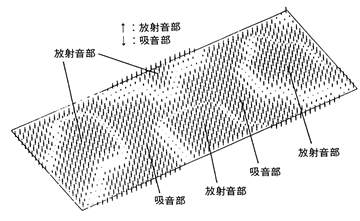
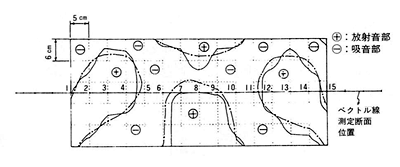
図12の実験はインテンシティレベルが0dBの時のコンタ線図であり、一点鎖線はクラドウニの図形の写しである。よく一致していることがわかる。
 |
 |

|
図13は図12の切断面の音の分布(2方向ベクトル合成結果)で、次のことがいえる。
1) クラドウニの図形線を境界線として、放射音部と吸音部の分離。
2) 吸音現象は板面近接位置で生じている(低周波ほど遠くまで生じる)板面から遠ざかるにつれて放射音のみになる。
3) 音の流れ方向、放射及び吸音現象は板の上下で対称的である。
図14は振動インテンシティによるPower Flowで、図12の放射音部の位置に集中して現われている。
振動インテンシティは、構造物の歪から発生するBending Waveのエネルギーと考えられる。このBending Waveは空気振動と整合すると、振動エネルギーを空中に伝達(音の放射)する。この意味で板面上の放射位置の直接測定をしている。